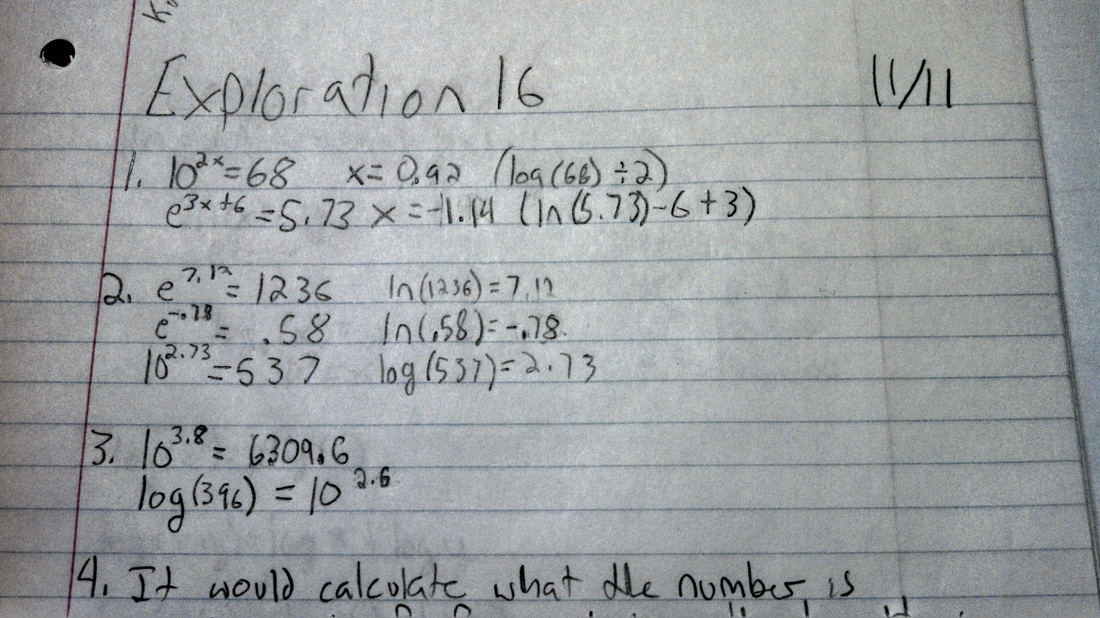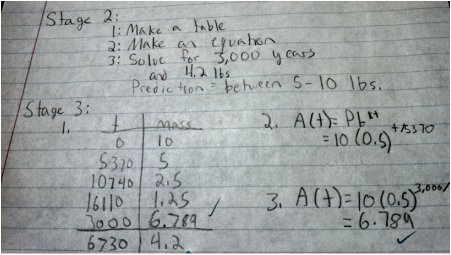Final Project Reflection
Generating ideas: I didn’t come up with the original idea for our zipline, but I know that I had come up with ideas of my own before we chose what we were doing. One of my ideas was to try and find the best chess strategy, but I didn’t think that that would work very well or be engaging enough. So while I can come up with ideas, it’s hard to follow through and knowing this I joined the zipline team.
Communicating thinking in a clear and accessible way: For our zipline, I helped design the small model and I drew some of the diagrams. I also did a lot of the math to figure out things like how much slack we need, where the stopping point should be, and how much rope that means we need. We didn’t end up using a lot of the calculations directly, in the end we just got more rope than we knew that we needed and figured it out from there.
Recognizing and resolving errors: For the final project, the main struggle we had was getting the materials to make the zipline. First we had to figure out what we needed, and to do that we looked up a lot of informational websites about how to make a zipline and how to tie good knots and such. When we looked up all of the parts we needed online, we found out that the cost would be too much, and we wouldn’t get them in time. So, eventually Dan brought in climbing gear that would work very well for the zipline, such as ropes, harnesses, and carabiners. That solved that problem, with a relatively simple solution.
Reflecting and synthesizing: This year the projects we’ve done have felt more true to real life, such as the taxes project and our final project. In real life people aren’t going to ask you how to find the side of a triangle just for math’s sake, but you might need to when you’re building a zipline. And the taxes project used equations to solve very real, adult parts of life, and it made people feel a little more prepared for the real world after high school.
Communicating thinking in a clear and accessible way: For our zipline, I helped design the small model and I drew some of the diagrams. I also did a lot of the math to figure out things like how much slack we need, where the stopping point should be, and how much rope that means we need. We didn’t end up using a lot of the calculations directly, in the end we just got more rope than we knew that we needed and figured it out from there.
Recognizing and resolving errors: For the final project, the main struggle we had was getting the materials to make the zipline. First we had to figure out what we needed, and to do that we looked up a lot of informational websites about how to make a zipline and how to tie good knots and such. When we looked up all of the parts we needed online, we found out that the cost would be too much, and we wouldn’t get them in time. So, eventually Dan brought in climbing gear that would work very well for the zipline, such as ropes, harnesses, and carabiners. That solved that problem, with a relatively simple solution.
Reflecting and synthesizing: This year the projects we’ve done have felt more true to real life, such as the taxes project and our final project. In real life people aren’t going to ask you how to find the side of a triangle just for math’s sake, but you might need to when you’re building a zipline. And the taxes project used equations to solve very real, adult parts of life, and it made people feel a little more prepared for the real world after high school.
Spreadsheet Workshop
Content Skill
Over the course of this semester, we have studied many different topics, but the one that I felt I got good at was the properties of logarithms. Logarithms are ways to find what exponent of 10 a number is. For example, 10 to the 4th power is 10,000, and log(10,000) is 4. The first time this was introduced, we entered values into a calculator, using the log button. Then, we had to figure out what the log button did, based on a couple of problems. Then we learned about some formulas, that log(c)=d, and 10^d=c.
|
Exploration 14 was the first time that we saw these kinds of problems, and then Dan gave us the formulas for it.
|
We got a lot more practice with logarithms.
|
Problem-Solving Skills
|
|Connecting an abstract idea to a real-world example |
One of the habits of a mathematician is connecting the math to real life, and I think that I got fairly good at that. In POW 3 we used math and equations to find the absolute value inequalities for a standard FIFA soccer ball.
|
|Formulating a Plan |
Another habit of a mathematician is creating a plan of action to find the answer to a problem. I was also not bad at this, shown in most POWs, but mostly in POW 5. In most POWs we have to generate a plan in step 2, and carry it out in step 3.
|